Emily M. Levesque, Guy S. Stringfellow, Adam G. Ginsburg, John Bally, Brian A. Keeney

SN2009ip is a particularly interesting "supernova" since it left a bright remnant behind, indicating that it was instead a supernova impostor.  The 2012B event, a brightening in late September 2012, looked like it might be a "genuine supernova", but maybe not.  Have a look at the other papers on this object: http://arxiv.org/abs/1210.3568, http://arxiv.org/abs/1210.3347, http://arxiv.org/abs/1209.6320. A few folks at CU, primarily Guy, had acquired some spectra of SN2009ip right around the 2012B event.  We had a quick look at the data and decided there was something really interesting in it that other groups (who probably had more complete data) had overlooked. The most interesting single point we noted was a peculiar "Balmer Decrement" (which is the ratio of H-alpha to H-beta).  The normal Balmer decrement is ~3 (2.87 at n~10³ and 10000K), but we observed a decrement of ~1.4 (and so did others, see e.g. http://users.northnet.com.au/~bohlsen/Nova/sn2009ip.htm). This Balmer decrement is weird, because all normal effects will increase rather than decrease the Balmer decrement.

• Interstellar reddening - affects the blue more than the red, therefore should decrease H-beta relative to H-alpha.  Of course, the reddening towards SN2009ip has been measured to be quite low.
• Line Splitting due to optical depth in the H-beta line (photons become "trapped" in the n=4 state and "escape" via Paschen-alpha and H-alpha) - but this only serves to decrease H-beta and increase H-alpha.  This is known as "Case C recombination" (see Xu et al 1992, Figure 1)

So what can increase the Balmer decrement?  Two possibilities:

1. Hydrogen reaches local densities above 10¹³ cm^-3: above these densities, it reaches collisional equilibrium with the gas and adopts the gas temperature.  At 10000K, H-beta will be a few times brighter than H-alpha [to-do: put exactly how much brighter...]
2. H-alpha becomes optically thick, while H-beta remains optically thin.  This is essentially a geometric argument, and is explored a little in the text.  If H-alpha becomes optically thick, more hydrogen won't increase the H-alpha brightness, but if H-beta remains optically thin, more hydrogen will increase its brightness.  Simple argument, and it hasn't been fully explored yet (does the radiative transfer work, or does the "Case-C" situation kick in too hard first?), but it is a plausible alternative.

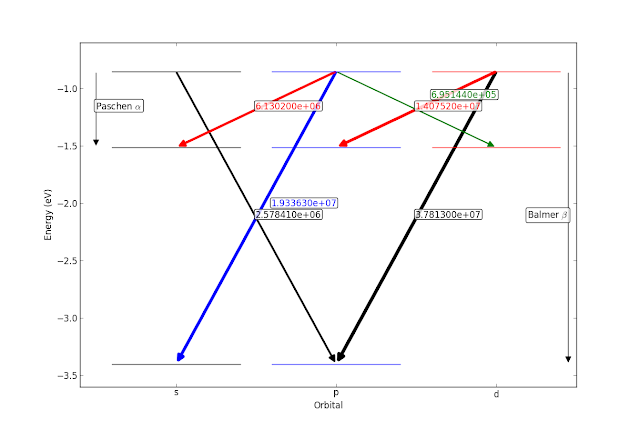
If you want to see my calculations in action, check out the ipython notebook performing the calculations. In case you're interested in Case C recombination, here's a first step: a hydrogen level diagram with levels connected by the (sum of the) Einstein A values between the relevant levels (from http://physics.nist.gov/cgi-bin/ASD/lines1.pl, generated with https://github.com/keflavich/energyleveldiagrams).