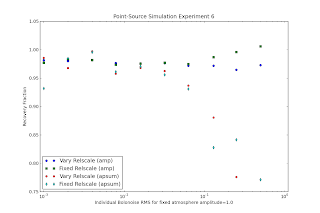
One clear simulation result comes from varying the amplitude of the gaussian noise added to each bolometer's timestream for a fixed atmosphere amplitude. The atmosphere amplitude sets the mean value of the atmosphere timestream. Increased bolometer noise results in decreased recovery of the outer rings of the PSF. This is demonstrated in that the peak amplitudes remain constant (as long as they are still recovered) while the aperture sums (in 100" radius apertures) decrease. The simulations were run on a logarithmic spacing from 1e-3 to 1e0. The 1e0 point is missing because the peak flux wasn't recovered by the gaussian fitter. The model maps don't recover the source at all for this run, which is worrisome, since it means there is no iterative process There is a minor concern that some simulations over-recover the peak at high noise, but the effect is at a <1% level so not very worrisome.

From the same set of simulations, I derive the pixel RMS of the map (the noise level) derived from a give individual bolometer noise. The theoretical expectation would be Measured Noise = Input Noise / N(bolometers) if the pixel sampling and the timestream sampling were the same (i.e. there were exactly sqrt(nbolos) hits per pixel). This is not exactly the case, and there are potential additional sources of noise. Nonetheless, the naive theory appears to be good enough in this simulation:

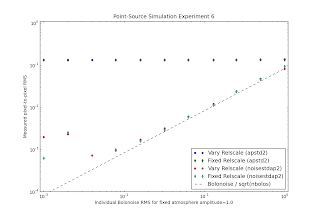
You can ignore the green/blue points in this plot; they just show that the std. dev. around the source is dominated by the source. Additionally, there is a noise floor, probably set by an inability to model the point source when the S/N gets to be ~500, preventing convergence of the iterator at a level better than 0.2%. In short, though, I'm going to use 1/sqrt(nbolos) to determine the appropriate input noise level in the astro simulations.