There haven't been many posts recently because I've primarily been writing up old results into the v2 paper. The Airy and Gaussian simulations with and without atmosphere seem to have yielded their results. There is a ~5% loss when mapping Airy-disk point sources. This is fine as long as it's quantified; it just means that when calibrating we need to know whether extended sources are similarly truncated. If all sources lose 5% in the pipeline, there will be no net offset. However, the Airy is not necessarily representative of the CSO's PSF. In order to come up with a more reasonable representation of the PSF, I've attempted to fit the *measured* PSF (from James' paper) with an Airy disk. The first sidelobe has a lot more amplitude and is closer to the peak than in an Airy disk. It is also asymmetric, but I'm ignoring that for the moment. To better represent the first sidelobe, I've fitted a modified Airy function. The "modification" is to fit two Airy functions, one to the peak and one to the rest. This is accomplished by setting everything outside the first null to zero in the first function, and everything inside the first null to zero in the second. The centers are the same, but the amplitudes and widths are independent.
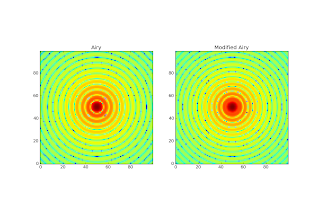
The above image shows the best fit Airy and modified Airy, both in log scale on an identical grid. The modeled PSF was then put through the pipeline to see it recovers the pipeline-derived PSF. The radial profile results are below, but note that this is only one particular realization of the simulation + pipeline.
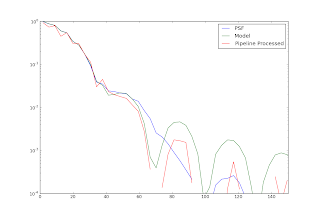
Note that the model matches the first sidelobe in the "observed" PSF pretty well, but both before and after pipeline processing, overpredicts the second sidelobe. There are a few "action items" remaining for this task:
- Re-derive the "observed" PSF using V2. Does it vary with epoch? Source?
- Find a model that better recovers the observed PSF
Any thoughts on better models to use? Does this seem like a good idea at all?