ADS arXiv An interesting examination of the morphology of the circumstellar material around IRAS 16594-4656. I did this work with Toshiya Ueta at the University of Denver. My contribution was azimuthally interpolating the 7 high-resolution long-slit spectra onto a 3-dimensional grid, creating a full 3D position-velocity cube. I used the Perl Data Language, which I have since abandoned.
[minor] Ongoing problems...
Since I have many tasks running in parallel, I need to summarize them sometimes...
- There are many "bad" observations that haven't been placed in "bad" directories. A list of the error messages generated is here: Making Infiles wiki
- There may be streaking in the BGPS ds2 images of l030 and l032. Still trying to re-run cleanly to find out
- There may be unflagged high-points in l030 and l032. Also under examination
- Simulations have been generating bulk-offset outputs; my suspicion was that the relative scales were being set incorrectly because astro dominated atmo, so I bumped up the atmo scale. The tests have run but I haven't examined the outputs
- V1 sims have shown streaking, possibly because of the previous bullet, but certainly (in part) because cross-scans haven't worked
Direct comparison of column-density power spectra
I've multiplied the 13CO integrated data cube, the Herschel 500 micron*, and the BGPS v1.0 and v2.0 by the appropriate conversion factor to get the maps into units of column density assuming T=20K and some opacity for the dust maps. BGPS v1 has been multiplied by the 1.5 "correction" factor.
- The Herschel maps are arbitrarily scaled; I didn't derive an actual column conversion but just guess-and-checked once or twice until I got something pretty close.
The power spectra look pretty outstanding:
The bumps and wiggles in the 50-200" range are quite well-matched in Herschel and Bolocam. Some map edge effects are visible in the Herschel maps, resulting in multi-frequency bumps at small spatial scales. The Herschel noise floor is also quite evidently lower. Also noteworthy is that BGPS v1 (scaled up by 1.5) matches the others "pretty well" but is a worse match, in general, to the Herschel data than is the BGPS v2. Here are some zoomed-in plots on the inverse scale:
And finally, the 13CO data is totally unrepresentative of the dust data. There is very little agreement on any scale. This may imply that the 13CO and/or dust temperature is too high, as a decreased T_D or T_ex will decrease 13CO column and increase dust column. However, it also raises a question - on what scales should dust and CO agree? This is getting into some real science, perhaps. The shapes of the CO and dust power spectra disagree: the CO is pretty well-fit by a power law, while the dust is not. What hypotheses can explain this?
There is a systematic temperature difference / preference in which CO or dust is hotter on the largest scales. -Dust is probably warmer on larger scales, however CO should be less abundant / more readily dissociated on these largest, most diffuse scales. CO shouldn't exist (or at least, should be underabundant) in regions with high temperature. Maybe? This probably needs to be quantified.
There is a systematic dust opacity difference on large scales resulting in lower dust emission.
- This is almost certainly true: the dust population increases in opacity with age, following OH94. Dust on the largest spatial scales should not have coagulated / collected ice, leading to a lower opacity on the largest scales
- This may also be true even though CO is present: dust coagulation is less efficient than CO formation at n~10^3-10^4 (I think - again, off the cuff, but consistent with OH94)
The CO overestimates all scales, either because of incorrect bulk abundance or temperature considerations.
- This is problematic..... if you drop the CO values at all scales, it becomes deficient in the 50-200 arcsecond range, where the dust measurements agree quite well
There is a preferred distance in both images
- It is not clear that the observed effects would occur because of this
- It is also quite evident from other analyses that there IS a preferred velocity, at least, and it completely dominates all others and has the same shape as the integrated power spectrum. So a distance effect is most likely ruled out.
Power Spectra of 13CO and Bolocam
Measuring preferred angles in the Herschel data on larger scales
This is something of a repeat of yesterday's exercise, but for Herschel data on larger scales, where filamentation is expected (at different angles?) on a different scale than the Galactic plane. First example: L030 500 microns
There is evidently a preferred direction that is correlated down to the resolution of the map, though the preference is smallest at the smallest scales. This may simply be a statement that there are more sources along the galactic plane, though, since there really isn't any particularly obvious filamentation in the image.
In L59, on the other hand, there is at most a very weak preference except at the largest scales corresponding to the Galactic Plane. This is somewhat interesting because there IS obvious filamentation in the L59 image, but it does not have a preferred direction. Unfortunately, it is not obvious whether or where filamentation shows up in fourier space if it does not have a preferred direction. There is no excess at any spatial scale that I can pick out.
Hunting for preferred directions
In our last group meeting, we discussed simulations using filamentary structures. I've been trying to determine how best to generate random/artificial filamentary structures in images. The first step in that direction is coming up with a way to measure asymmetries and therefore preferred directions within a real map. In order to do this, I've had to develop a number of new tools in agpy for azimuthally binned radial profiles and radially-averaged azimuthal profiles (radialprofile.py). Examining real maps is necessary because a simple sinusoidal dependence of the power introduces filamentation along the same directions at ALL scales, which is not obviously (or in some cases, obviously not) the correct solution. Filaments are observed on large scales, but sometimes there can be 'kinks' in opposite directions on small scales. So, the map I picked to examine was one with the most flagrantly obvious filamentary structure in it: the Motte DR 21 MAMBO map. It was also a choice of convenience because I already had the data on my laptop....
The preferred direction is quite obvious in this map: there is a long filament going up and down the map. Therefore, the DC component should be substantially higher in one direction than the other.
In the power-spectral-density image, it is quite clear that there is a preferred direction, though it is not obvious that the fourier transform is rotated 90 degrees from the image. My fourier intuition somewhat fails me here.... I realize that a broad, smooth profile in real space should be narrow and highly peaked in fourier space, but I don't fully understand why it effectively spreads out in the perpendicular direction, which I have confirmed that it does with a simple experiment. I also don't know what the Shah function is, but it implies a periodic dip in the image at every 1/5th of the image, or every 50 pixels.
These are the power spectra averaged over different angles as labeled. -15 corresponds to -15 to +15, 15 corresponds to 15 to 45, etc. The highly peaked 75-105 power spectrum shows the large-scale filamentary profile. I think the difference in the DC component is actually an artifact of the azimuthal binning process: each pixel can only be assigned one angle, so the DC value isn't included in all of them... I'll need to find a workaround for that because it's quite deceptive.
The more interesting way to view the data - and perhaps to analyze maps - is to take radial averages in some range of spatial scales and plot the azimuthal dependence. There is a clear sinusoid at large scales. The legend shows "spatial frequency" in 1/pixel units. The distribution becomes more even with angle and even changes preferred direction at smaller scales (higher frequencies). Next step is testing different approaches. I think an added, steeper-power-law component would probably be the best way to start. Another suggestion, courtesy Bruce Elmegreen, is to attempt this sort of asymmetric power law sampling in 3 dimensions (with only 1 or 2 dimensions asymmetric) and then projecting down onto two dimensions.
Updates for 6/1/2011 meeting
This is going to be a mishmash of various things.... First, Jared has run the same simulations I e-mailed out through the V1.0 pipeline. Unfortunately, the results are not good - there is substantial streaking of a variety not seen in the real data in V1. Second, here are the simulated images from V2: http://eta.colorado.edu/bgps/simulations/Experiment7_Simulation_Images.pdf Unfortunately I can't present a direct comparison because something got screwed up...
Recovery as a function of bolometer noise part 2
In the Experiment 7 simulations I was running, I observed greater noise than expected, causing me to question the results of the previous post. I therefore ran Experiment 8, which is the same as Experiment 6 from that post with a larger (320x320) map with a larger step size. The noise recovery remains linear, but the scaling is quite different - a factor of ~4 instead of ~12. The step size is the most likely culprit, since an 8x larger step size should result in sqrt(8)~2.8 worse noise per pixel.
There are some curious / worrisome artifacts that turn up and are evident in the recovery fraction plot. For the low-noise cases, the middle bolometers get totally flagged out because they are over-weighted (by orders of magnitude).
So I'm forced to explore via pyflagger. I will almost certainly need to re-run all experiments after making a change to how weights are computed. Well, it turns out the problem is that those 28 bolos are scaled to zero, even though there is nothing obvious (or even suggestive) in their timestream plots. This is only true when varyrelscale is off. Apparently varying the relative scales leads to a different problem. AHA! The noise is so low that the relative scales are SO well correlated that the signal is enough to cause problems! A plausible solution is therefore no change to the pipeline, but to add minimal (nominal) noise to the relative scales to increase the MAD so that the others don't get flagged out. So I added a 1% variation, which prevented flagging at the scale stage, but there are still some disturbing artifacts in the map:
Unfortunately, this problem requires further examination in detail. Exp 9/10 should probably be gaussians and airys on larger step-size maps, but the solution will require something else, possibly even a change in the pipeline. On the plus side, I think I can re-run experiment 7 with a factor of 4 instead of 12 scaling for the noise and expect it to work.
Recovery as a function of bolometer noise
One clear simulation result comes from varying the amplitude of the gaussian noise added to each bolometer's timestream for a fixed atmosphere amplitude. The atmosphere amplitude sets the mean value of the atmosphere timestream. Increased bolometer noise results in decreased recovery of the outer rings of the PSF. This is demonstrated in that the peak amplitudes remain constant (as long as they are still recovered) while the aperture sums (in 100" radius apertures) decrease. The simulations were run on a logarithmic spacing from 1e-3 to 1e0. The 1e0 point is missing because the peak flux wasn't recovered by the gaussian fitter. The model maps don't recover the source at all for this run, which is worrisome, since it means there is no iterative process There is a minor concern that some simulations over-recover the peak at high noise, but the effect is at a <1% level so not very worrisome.
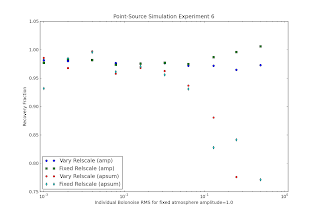
From the same set of simulations, I derive the pixel RMS of the map (the noise level) derived from a give individual bolometer noise. The theoretical expectation would be Measured Noise = Input Noise / N(bolometers) if the pixel sampling and the timestream sampling were the same (i.e. there were exactly sqrt(nbolos) hits per pixel). This is not exactly the case, and there are potential additional sources of noise. Nonetheless, the naive theory appears to be good enough in this simulation:
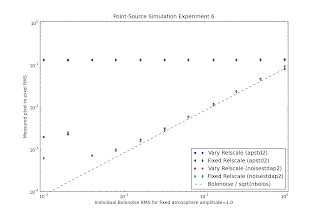
You can ignore the green/blue points in this plot; they just show that the std. dev. around the source is dominated by the source. Additionally, there is a noise floor, probably set by an inability to model the point source when the S/N gets to be ~500, preventing convergence of the iterator at a level better than 0.2%. In short, though, I'm going to use 1/sqrt(nbolos) to determine the appropriate input noise level in the astro simulations.
Astrophysical Signal Modeling
Here we finally get into the meat of the simulations. The goal is to develop realistic - but arbitrary - astrophysical models to run through simulations. The first step is to figure out what a realistic sky looks like. To this end, I use the HiGal SDP fields, looking only at their power spectra. They are well represented by a power law with α = 3 (shown in the dashed black line below).
Therefore, I've attempted to randomly sample from a similar power law distribution using the following IDL code:
dimsize = 512 realpower = realpowers[ii] imagpower = imagpowers[ii] imagscale = imagscales[ii] peakamp = 1.0 noise = 0.03 smoothscale = 2.0 smoothkernel = psf_gaussian(npix=512,ndim=2,fwhm=31.2/7.2/2.0,/normalize) sigma_gp = 128.0 ; sigma-width of the Galactic Plane (can get more accurate value from Cara's paper) xx = findgen(dimsize) # replicate(1.0,dimsize) yy = findgen(dimsize) ## replicate(1.0,dimsize) rr = sqrt( (xx-255.5)^2 + (yy-255.5)^2 ) realpart = (rr^realpower) * randomn(seed1,[dimsize,dimsize]) imagpart = ((rr*imagscale)^imagpower) * randomn(seed2,[dimsize,dimsize])*complex(0,1) fakesky = abs(fft(shift(realpart + imagpart,0,0),1)) expweight = exp(-(yy-255.5)^2/(2.0*sigma_gp^2)) ; most power is in the inner plane fakesky *= peakamp/max(fakesky) fakesky_sm = convolve(fakesky,smoothkernel) fakesky_sm = fakesky_sm*expweight fakesky_sm += randomn(seed3,[dimsize,dimsize]) * noise
Since Power is the fourier-transform squared, I'm using a power-law of α=1.5 for the "real" part of the sampling. The imaginary part follows a shallower slope to reduce the amount of power in large structures, which didn't look quite right (but maybe I should leave both slopes the same?). With both the same, and without the imaginary part down-scaled, the structure appears too "cloudy" and not "clumpy" enough. But back to that later...
The peak amplitude is set by re-scaling the map. Ideally, we'd like to see this set by a point source, since that is true in most fields. The noise level should not be included in simulations, but should be used to show the difference between pipeline-leftover noise and gaussian noise on the sky. i.e., what structures disappear when you just add noise, and what structures are removed by the pipeline.
The PSF is simply to smooth out signals that are removed by the telescope beam. We can replace this with a "real" PSF if and when we've come up with a believable one.
The noise is added after the smoothing because it should be on a pixel scale rather than a beam scale.
Here are some example realizations with different power laws:
