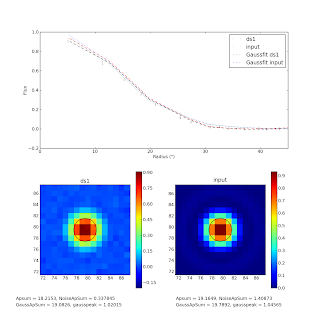
We noted in discussion yesterday that the aperture sum in the (nearly perfectly recovered) is lower than expected even for a gaussian fit of an airy. A Gaussian approximation to an Airy should recover 93.5% of the flux; 6.5% of the power is in the sidelobes of an Airy disk. We recover about 86-88% of the flux in the input point-source map, or about 5-7% short, despite matching the peak to within 2-3%. This discrepancy is partly - but not completely - explained by a slight negative bowl effect: the Gaussian fit has a higher total flux than the aperture sum. Using the gaussian fit value, the recovery is about 90%. A mere 3% missing flux is not too much of a problem - it could still be that the gaussian is uniformly reduced by bowl effects, or perhaps that some flux is not reincorporated into the map (at a very low level) because it is correlated enough to be PCA-cleaned. In the figure, the top panel is the radial profile of the ds1 data (black), the input data (red), and their gaussian fits (see legend). The circles on the labeled images show the FWHM of the fitted gaussian, indicating a good fit. The apertures used for summation are NOT displayed. The sum aperture has a radius of 90" (6.25 pixels) and the "Noise Aperture" has the same area as the sum aperture.

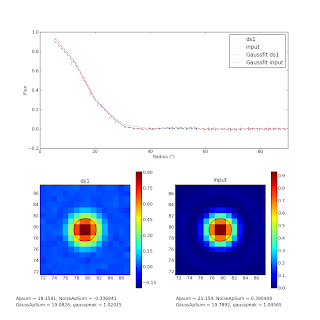
If we redo the analysis with a smaller aperture, the recovery is better: 95% in the central 45". However, now the airy ring cannot account for any lost flux, so it still looks like there's a 5% loss intrinsic in the pipeline.