As you'll recall from my previous post (and references therein...), the 2005 Orion data shows a discrepancy between ds1 and ds5 data in which the ds1 data is significantly (~10%) higher than the ds5 data. However, the 2010 Uranus observations show much larger discrepancies between ds1 and ds5 favoring the ds5 data! Because that was somewhat unbelievable to me, I ran ds1-ds5 comparisons on Uranus data from other epochs, and discovered that ds1>ds5 uniformly (also, it looks a LOT better). So, the question remains, WHY is the Dec 2010 data brighter in ds5? More confusing to me, why do the ds5 PSFs from 2010 look so reasonable, while the ds5 PSFs from all earlier epochs look terrible? For example, I use the observations 070727_o31 and _o32. These show clearly the blurring and flux-loss that happens when ds5 data are used for 'normal' point-sources:
From a comparison of 3 different epochs using abou...
From a comparison of 3 different epochs using about a dozen different reduction techniques, but all with pairs of cross-scans, ds1 is uniformly higher than ds5. The only thing left to do is compare the individual scans, I suppose... if the cross-scans behave differently, that explains the difference between 2010 and other epochs
Downsampling - what is going on?
The downsampling failure I noted previously appears to be illusory. It may be that the offset noted only holds for single-frame images, in which there may be many blank pixels. It is possible - though not certain - that the ds1 images were significantly higher than ds5 because more noise-only pixels were included with higher outliers; i.e., ds1 high-outlier noise was being compared to ds5 noise that was lower amplitude.
What led to these conclusions? First, I was getting inconsistent results looking at Uranus in particular - ds5 appeared to have higher fluxes than ds1. This was inconsistent with earlier results on OMC1. Partly, this is because I switched from my hacked-together plots to the much more refined compare_images script, which demonstrated the effect of changing the cutoff of the comparison.
Also, I added in a Pearson Correlation Coefficient computation. Given a single data set with the only difference being downsampling, the data should be perfectly correlated even if there is a flux offset (correlation should be 1, but the best fit slope should not be). It was an indication of a problem when I started seeing correlation coefficients <0.90 for data that had already been sigma-cut; that means that noise was being included in the correlation computations.
Therefore, the approach needed is to cut out the high pixels that are on map edges. This I accomplished by adding an 'aperture' capability to the compare_images code (for Uranus) and cropping using montage and a wcs-based box for Orion.
The results... are ambiguous. Wow. In some sub-fields - within the same co-added map - the agreement is near-perfect.

In others, ds1 is clearly > ds5.

What's going on? ds1 does look uniformly more smooth. Note that the disagreement is nearly scale-free:
OK, so given the conclusion in Orion that ds1>=ds5, what's the deal with Uranus?

The first two comparisons are for 1x1° observations; in both cases ds1 < ds5, but by 6% and 24% respectively! The image of Uranus looks much better (because of lack of parallel lines) in the second, more extreme case. In both cases, the ds5 excess is nearly scale-free (not shown).


The 3x1s are also highly discrepant. #12 shows nearly perfect agreement, albeit with high dispersion (low correlation) because of pixel-to-pixel variations around the peak. #13 is the only observation with a huge DS1 excess. It also demonstrates very poor correlation. It looks like the telescope got bumped for the ds5 data (which is not actually possible; recall they're the same data set). What happened here? Maybe a glitch that went unflagged (mad_flagger is off by default for individual scans)?


In observations 4 and 5, we're looking at a 40-50% excess in ds5! What the heck? There really is no clear explanation for this.


But... what? Magically, they come into perfect agreement when the scan axis nearly lines up with the coordinate axis! Or, is this just an effect of the worse weather on night 2?

Next thing to try: masked source map comparison. Unfortunately, masking royally screwed up the long scans - probably because the initial polysub didn't work. And masking in the individual point source maps did nothing... so that pretty much rules out atmospheric oversubtraction, doesn't it? What else could be causing this offset? 0pca looks the same as 13pca, give or take, so it's not the atmospheric subtraction. Could the downsampling result in an offset in the bolo-scaling? Where else in the process could things go wrong? Tomorrow, need to investigate .sav files with pyflagger...
Making maps faster
The fundamental problem at this point is making the pipeline run faster. At current speeds, with undownsampled data, it may take ~days to process a single map. Ideas for faster processing:
- Find out how long it takes to converge to 1%, 5%.... If it only requires 10 iterations, that's a factor of 2 savings over current strategies.
- Use downsampled data of some sort if possible. Does DS2 match DS1? How do we measure it? Flux-flux comparison and PSF point-source size measurements are the most important. Need to automate PSF comparison....
- Can we use median-combined individual images as a 0th order model? I bet the answer is 'yes' and will probably increase the speed of convergence by a large amount. Tests to run? This is probably needed if we are to split up the 'super-fields' into smaller sub-fields, otherwise overlapping data will be used less effectively.
- Find some way to keep bgps.raw, bgps.ra, bgps.dec, and other items that are only used once on the HD during the iterative process. Is there any way to separate out data in a struct in this manner?
Delining - Maps
First comment - delining has no effect on downsampled data. At least for the 0709 epoch, there were NO lines AT ALL in the data. From 0-5 Hz, it was just empty. So we don't have to worry about that... the problem only affects fully-sampled data. Then, onto map comparisons. Curiously, the noise levels don't drop after delining. They actually go up a bit. This may be because of the effects on PCA cleaning. However, flux levels in the sources go up by 0-10%. As usual, the change in flux changes from field to field without any obvious reason. Example 1: A pointing field. The source is ~2% brighter in the delined version, but otherwise the match between the two is nearly perfect.


Example 2: A bigger map, where the flux recovery is much greater when delining, but the background levels are also higher.


Delining and the Cleaning process
One item I forgot to mention last night was the effects of lines/delining on PCA subtraction. These should be the primary effects on the final map for all epochs except 2010, in which case the primary effect SHOULD be to reduce substantial noise. In the examples below, there are PSDs of whole timestreams (left) and example timestreams from single scans (right). The first thing to note is that the delined timestreams still have correlated components in the line region, but they are suppressed - their amplitudes, and therefore their sort order in the PCA removal scheme, are changed. Since PCA cleaning is by its nature adaptive (the number of components remains fixed, but the order changes), these effects can be significant and dangerous. If the line noise is more correlated, a PCA component will be dedicated to removing it instead of atmospheric signal. Below are examples from l089 (epoch 0709) first. These have less correlated line noise and are more typical of BGPS observations. The first PCA component, the average, does not change much with PCA cleaning. However it is clear that the second component changes substantially, from large-amplitude high-frequency noise to small-amplitude variations that are very likely to describe atmosphere.
Example 1 - Zeroing out the lines:


Example 2 - Fitting and removing the lines:


Example 3 - Suppressing the lines with a non-fitted Gaussian:


The next examples are from December 2010 observations of Uranus. In this case, the correlated noise component is clearly dominant.
Zeroing lines:


Fitted lines:

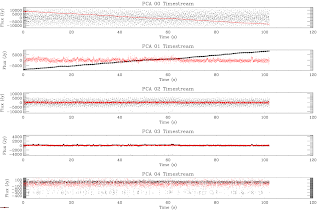
Non-fitted gaussian suppression:


Finally, these two are demonstrations of what you might expect to see for a purely noiseless images of a planet (it was constructed from a PSF). PCA is first:


A single bolometer's timestream and PSD:


Delining
Delining refers to the process of removing electronic noise that is aliased to particular frequencies by the discrete sampling of the data. Typical electronic noise is at 60 Hz with some width. It gets aliased to these frequencies: linefreqs = [10.05+findgen(10)*1.2,10.05-((findgen(7)+1))*1.2] The 10.05 Hz and 20.10 Hz are the worst in most cases, and they are wider. For the above lines, we "remove" a bandwidth of 0.09 Hz by averaging over the neighboring 0.5 Hz on either side. For the wider lines, we remove 0.5 Hz by averaging over the neighboring 1.5 Hz on either side. There are a few new things about the delining process that did not exist in James' old version:
- The wide-band lines are removed
- A check is performed before removing the lines - they are only removed if the line region mean is 2-sigma above the average region (as computed via median and mad)
- The replaced noise is computed via median/mad, and the new noise level is set 5x lower than in the neighboring region
Now, some examples:


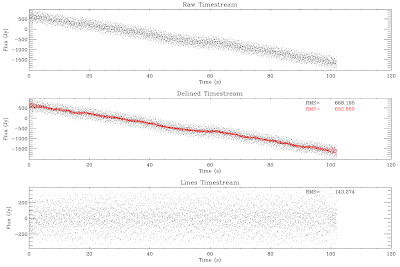
The timestream (left) and PSD (right) of a "pretty good" bolometer. There is a lot of noise in lines, but note that the peak power is 2-3 orders of magnitude below the PSD peak. In this case the "Power" is in Jy. There is little astrophysical information below ~14" (9 Hz), and there should be none below 7.2" (17 Hz), but there is plausibly information at these scales. It therefore makes sense to save as much information as possible. As can be seen in the delined PSD, the peaks drop by a substantial fraction, but not all the way - that's because these lines are wider than typically observed. Unfortunately, I don't have any really good ideas about how to fix this issue - I think fitting gaussians to each line, while attractive, is going to be prohibitively expensive in both programmer and processor time. However... it would be a very interesting project to undertake. In the timestream, it can be seen that the RMS drops substantially when the lines are filtered out (note that the timestream is strongly dominated by large-scale structure, so 'substantial' is really based on the RMS of the lines removed).


The next two plots look identical to the previous ones. In principle, they include the wide-band delining. However, in this case, the satellite lines to either side of the 10 Hz line are too strong and prevent identification of the 10 Hz line. This is unfortunate, again, but no obvious solution presents itself.


Now we come to a truly problematic bolometer. The lines completely dominate the power spectrum. Narrow line removal fails.


Wide line removal does a much, much better job, dropping the RMS by an order of magnitude.... but the bolometer probably still needs to be removed, since the astrophysical signal is 2-3 orders of magnitude below that.


The 2010 data had much worse line noise and had to be delined. JS accomplished this by throwing out all data above a certain frequency, but I prefer the delining approach. It is clearly effective, but again leaves much to be desired. Should the flagged bandwidth be increased? What about the extra lines around 18 Hz?

Again, the wide line flagging fails because of the satellite lines.
Next step: prove that this works in maps...
Next step: prove that this works in maps...
Some pretty neat things about delining....
Well, I did the work, so might as well come up with some plots... I created a gaussian-fitting based delining code that saves all of the fits in a text file! That's a lot of data to play with, and allows me to draw some conclusions:
- For the narrow lines, the linewidth (gaussian sigma) is 0.03 Hz. For the wide lines, it is 0.05.
- The amplitudes from December 2010 are ENORMOUS compared to others!
- The width distributions of the two are similar, though the lines appear to be significantly wider in July 2009
I've also gotten to the point that I'm satisfied with how delining with wing suppression works. Wing suppression is 0.4-2x quicker than fitting directly, depending on... not clear what exactly; it depends on epoch, but that could either be because there are more lines found or because of relative data size. Does delining have to be done on whole timestreams, or can it be done on a scan-by-scan basis? This is not entirely clear... the peaks are less suppressed when done on a scan-by-scan basis (presumably because the S/N is low and peaks are therefore not detected), but incorrect suppression (removing a line that's not there) is reduced. For short scans, the scan-by-scan approach is 10x faster; for longer scans it's ~20% faster. I think the scan-by-scan approach is going to be ideal.
Examples from l089 (0709): Top row: non-fitted line suppression


Bottom row: fitted line suppression


Examples from Uranus (1012, really really liney):
Top row: non-fitted line suppression


Bottom row: fitted line suppression


Bleh, a whole day's work dedicate to new delin...
Bleh, a whole day's work dedicate to new delining methods and testing. Very unrewarding. However, there are results that I need to FINALLY prove and show tomorrow: 1. amplitude suppression + phase preservation is a good alternative to zeroing/scrambling or replacing with noise 2. line fitting is effective but slow 3. Assuming a line profile and suppressing is nearly as effective as line fitting 4. scan-by-scan is less effective than observation-by-observation for fitting (but it's not clear if that holds for other methods)